A nice puzzle this week, via NRICH’s magnificent @ajk44: a semicircle is inscribed in a 3-4-5 triangle as shown. Find $X$.

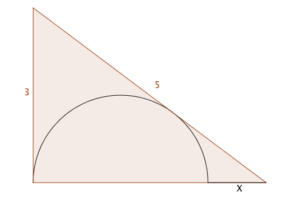
Insemicircle puzzle

I think it’s a nice puzzle because Alison’s way of doing it was entirely different to mine, but thankfully got the same answer. You might like to try it yourself.

My way

My way was to consider similar triangles. Draw a perpendicular at the point of tangency, T; that crosses the ‘4’ side at the centre, C. Now, the triangle ATC is similar to the original triangle (it also has a right angle and shares the angle at A, so all three angles are the same.)

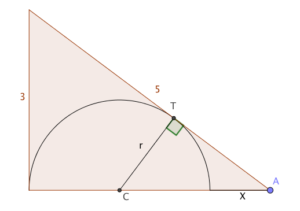
Supporting triangle

In particular, that means $\frac{r}{r+X} = \frac{3}{5}$. We also know that $2r+X = 4$, because of how the base is split up.

Writing the first fraction as $\frac{2r}{2r+2X}$ to make the substitution easier, we get $\frac{4-X}{4+X} = \frac{3}{5}$, and it’s clear that $X=1$.

Alison’s way

Alison’s way was neater, I think. She used the Equal Tangents theorem (the one I mentioned last week) to spot that $T$ splits the hypotenuse in a ratio of 3:2.

Using the same triangle as me, she got $\frac{r}{2} = \frac{3}{4}$, so $r = \frac{3}{2}$ and $X = 1$.

A third way

If you’re a coordinate geometry sort of person, you might wonder about the equation of the hypotenuse and of the semi-circle. The hypotenuse is $4y+3x=12$, assuming the right angle is at the origin, and the semicircle is $(x-r)^2 + y^2 = r^2$, for some unknown value of $r$.

Those two can be combined into a quadratic - and for the right value of $r$, it will have only one solution.

Multiplying out the semicircle gives $x^2 - 2rx + y^2 = 0$. I’d multiply that through by 16 to give $16x^2 - 32rx + (4y)^2 = 0$, reasoning that I can then easily substitute $4y = 12 - 3x$ into it.

Expanding, $16x^2 - 32rx + (12-3x)^2 = 16x^2 - 32rx + 144 - 72x + 9x^2$.

Simpifying: $25x^2 - (32r + 72)x + 144 = 0$.

This needs to have a repeated root, so its discriminant must be 0: here, $b^2 - 4ac = (32r + 72)^2 - 14,400$

So, $(32r + 72)^2 = 14,400$, which means $32r + 72 = 120$, or $32r = 48$. Aha! $r = \frac{3}{2}$ as before.

I’m sure there are other, equally nice, approaches. What other ways might you attack it?