Dear Uncle Colin,

I find it easier to remember trigonometric identities if I can ‘see’ how they fit together. I’m expected to know that $\sin(2x) \equiv 2\sin(x)\cos(x)$, but haven’t been able to prove it. Any ideas?

-- Geometry? Right Angles? How About Medians?

Hi, GRAHAM!

My favourite proof jumps out from a picture like this one:

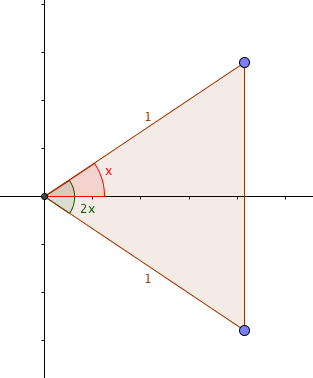
Screen Shot 2016-03-29 at 21.29.22

Draw a right-angled triangle with hypotenuse 1 and an angle $x$; then draw its reflection in the adjacent side (so you have an isosceles triangle with angle $2x$ at the apex), as above.

Now, the sides of the triangle are 1, 1 and $2\sin(x)$, at the base; the angles are $\left(\frac{\pi}{2} - x\right)$, $\left(\frac{\pi}{2} - x\right)$ (both at the base on the right) and $2x$ (at the apex on the left).

Using the sine rule, $\frac{1}{\sin\left(\frac{\pi}{2}-x\right)} = \frac{2\sin(x)}{\sin(2x)}$

Cross-multiply: $\sin(2x) = 2 \sin(x) \sin\left(\frac{\pi}{2}-x\right)$.

Since $\sin\left(\frac{\pi}{2}-x\right) = \cos(x)$, that means $\sin(2x) = 2\sin(x)\cos(x)$. With a tombstone!

-- Uncle Colin