The smart way to do the binomial expansion (Part 1)

Ah, the binomial expansion. The scourge of my A-level: the sum that was always wider than the paper, and always had one more minus sign than I’d allowed for. A crazy, pointless exercise in arithmetic, if you ask me, only really useful for finding square roots in your head (of which more another time).

What is the binomial expansion?

Let’s say you have to work out something like $(2-3x{)}^7$. The naive way of doing that is to write out $(2-3x)$ seven times and multiply all of the brackets together - which takes weeks, of course.

There’s a simpler way - the binomial expansion - which tells you how to work it out in many fewer steps. It’s given to you in the formula book as: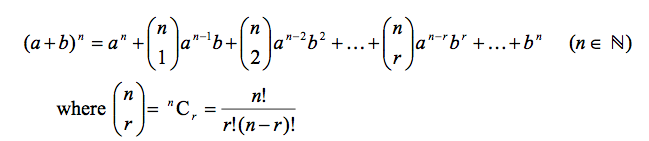

You’re allowed to recoil in horror, but it does make things a bit simpler… but it’s still a mess. In this article, I’ll show you how to break it down into easy bits - and lay it out so you have plenty of paper.

Making a table

The most useful bit of the formula is actually the most horrible bit. It’s the bit between the dots - the ${}^n{C}_r{a}^{n-r}{b}^r$ bit. That actually tells you everything you need to know (maths is like that: a language for expressing complicated ideas very concisely).

What it tells you is that there are three parts to each term in the binomial expansion:

• A number from Pascal’s triangle (the ${}^n{C}_r$);
• A power of the first thing in the bracket ($a^{n-r}$); and
• A power of the second thing in the bracket ($b^r$).

These are going to be the first three columns of the table - I like to call them C, A and B - and we’ll have a fourth column as well, which is CAB - the three things multiplied together.

The first column

The first column is the numbers from one of the rows in Pascal’s triangle - the one that has the second number being the power you’re putting the bracket to (I’ll call that $n$). If $n$ is below about six, it’s easy enough to draw out Pascal’s triangle if you know what that is; any higher than that and it gets a bit error-prone.

In any event, you can get the number out of your calculator using the ${}^n{C}_r$ button - on my calculator it’s shift and ÷. The top row is ${}^n{C}_0$, the next one is ${}^n{C}_1$ and so on, all the way up to $n$.

(If you’re studying C4 and have your hand up to say ‘it doesn’t work with negative or fractional powers!’ - yes, I know. There’s a Part II coming soon. Just hold tight, get used to this way and it’ll just need a small change.)

For the example I mentioned earlier, $(2-3x{)}^7$, your $n$ is 7. That makes the first column 1, 7, 21, 35, 35, 21, 7, 1.

The second column

The second column is the one corresponding to $a^{n-r}$. What that means is, you take the first Thing in the bracket (here, it’s $2$), start by putting that to the $n$th power, and drop the power by 1 each time - effectively dividing by the Thing. So, you start from $2^7=128$ and halve it each time. (When $n$ is a positive integer, this will always end at 1). Here, you get 128, 64, 32, 16, 8, 4, 2, 1 in the second column.

The third column

The third column corresponds to $b^r$. This means, take the second Thing in the bracket (including any minus sign - here it’s $-3x$), start by putting it to the zeroth power and add one to the power each time - same as multiplying by the Thing. The third column here would be $1,-3x,9x^2,-27x^3,81x^4,-243x^5,729x^6,-2187x^7$.

The final columns

Lastly, for the CAB column, you just multiply the three Things in each row together. Here’s how it looks:

C	A	B	CAB
1	128	$1$	$128$
7	64	$-3x$	$-1344x$
21	32	$9x^2$	$6048x^2$
35	16	$-27x^3$	$-15120x^3$
35	8	$81x^4$	$22680x^4$
21	4	$-243x^5$	$-20412x^5$
7	2	$729x^6$	$10206x^6$
1	1	$-2189x^7$	$-2189x^7$

… and the only thing that remains to do is to write out the whole thing in one line (if you can fit it): $(2-3x{)}^7=128-1344x+6048x^2-15,120x^3+22,680x^4-20412x^5+10206x^6-2189x^7$. Job done!

(You’d be really unlucky to get anything that big in an exam - the worst case scenario for the ‘whole thing’ is $x^5$, or you might be asked for the first three or four terms of a bigger power. In that case, you just end the table after four rows, easy!)

* Part 2 in the series is here.

* Edited 2016-12-28 to add a link.

* Edited 2021-06-15 to fix a table.