A puzzle in Turkish
This one came to me by way of @blatherwick_sam:
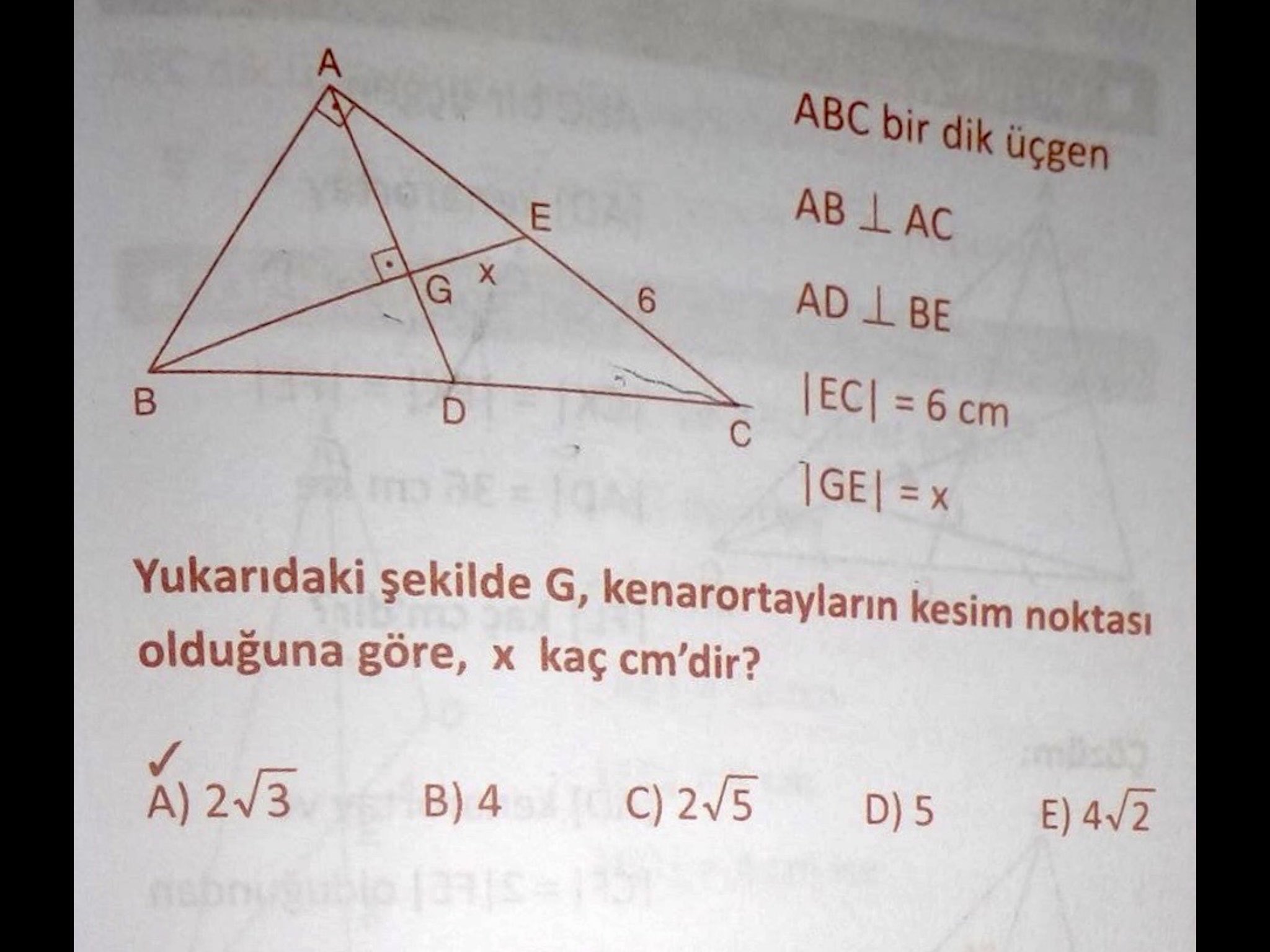
— matematik (@il1123) June 19, 2021
Now, my … presumably Turkish? … is not even rudimentary. It might be that yours is better, but maths is the universal language, right?
In any case, have a crack at it, and I’ll share how I solved it below the line where – obviously – there be spoilers.
My first approach
I started with a big picture, of course. I picked out some angles, labelled them. I figured out some ratios, gave things names. I even threw some trig at it. All to no avail.
So I went back to the tweet for a hint.
“Missing” information
Or rather, some information I hadn’t picked up: G is the triangle’s centre of gravity. (I wonder if I could have deduced that.) That makes everything simpler.
For a start, it means that AE and EC are the same length, and it means that BG is twice the length of GE (so, $2x$).
Because of the right angles, triangles AGE and BGA are similar, so AG works out to be $x\sqrt{2}$; a little bit of Pythagoras says that AE must be $x\sqrt{3}$ long.
So $6 = x\sqrt{3}$ and $x = 2\sqrt{3}$, which – fortunately – is one of the answers.
Reflection
The key bit of problem-solving here was to ask what information am I missing? – it has friends like “what would make this simpler?” and “have I understood everything in the question?” – and once I had that, everything dropped out.
Did you tackle it a different way? Do let me know!