Ask Uncle Colin: Incircles

Dear Uncle Colin,

I noticed that the incircle of a 3-4-5 triangle has a radius of 1, and for a 5-12-13 triangle, it’s 2. Is it always an integer in a Pythagorean triangle?

Having Elegant Radius Or Not?

Hi, HERON, and thanks for your message!

It turns out that yes, the incircle of a Pythagorean triple always has an integer radius. The key to the problem (for me, at least) is the equal-tangents theorem.

A picture

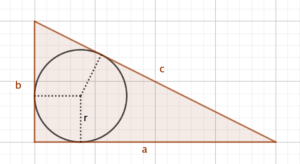
Looking at this diagram, you can see that the two tangents that meet at the right angle must have length $r$.

The other vertical tangent must have length $b-r$; the other horizontal tangent must have length $a-r$.

Because two tangents meeting at a point have equal length, the upper-left portion of the hypotenuse must also have length $b-r$, and the lower-right portion also $a-r$.

But, those two together make $c$, so $(b-r)+(a-r)=c$, which rearranges to $a+b-c=2r$. (This is consistent with both of your observations).

But is $r$ an integer?

This isn’t quite enough: we still need to show that $a+b-c$ is even!

And it is, of course: because it’s Pythagorean - $a^2+b^2-c^2\equiv 0(\mathrm{mod}2)$; meanwhile, $x^2\equiv x(\mathrm{mod}2)$, so $a+b-c\equiv 0(\mathrm{mod}2)$ - so it is indeed even, and the incircle radius is always an integer!

Hope that helps,

- Uncle Colin