Daylight, Durlston Castle, and Where is Hamburg?
“Is Hamburg that much further north than London?”
I furrowed my brow. Hamburg, to the best of my knowledge, is not that much further north than London. But here it was, written in stone (on the side of Durlston Castle in Swanage.)
(I’ve transcribed the sign at the bottom of this post).
Things were about to get geometric.
Colin’s model Earth
My model of Earth is not as large as the Large Globe, a short walk from where we were, but that makes it much more portable. I can carry it in my head.

It consists of a sphere of unit radius (because “Earth radius” is a perfectly good unit to measure the Earth in), with a plane cutting it at an angle of (up to) 23.5º ((Yes, degrees are the standard unit for measuring the planet. I don’t like it, but I have to go along with it.)) to the vertical, passing through the centre of the sphere.
Each line of latitude is a horizontal circle, with radius $\cos(\lambda)$, where $\lambda$ is the latitude.
The Longest Day
In fact, we’re looking at the longest day of the year, when the angle is 23.5º. Now, I happen to know the latitude of London, it’s about 51.5º north of the equator, which makes the radius of its circle of latitude $\cos(51.5º) \approx 0.623$.
Where does the day/night plane cut the circle? A diagram will help here.
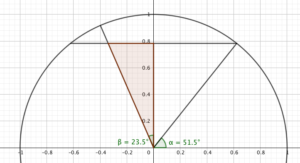
We’re trying to find the shortest leg of the red triangle. Its longer leg is $\sin(51.5º)$, and the angle at its base is 23.5º, so the leg is $\sin(51.5º)\tan(23.5º)$.
So, how much of the line of latitude is in shadow at solstice? Another diagram will help.
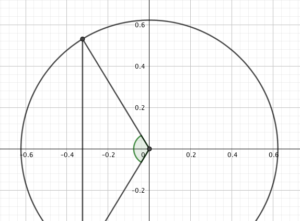
Now we’re looking down on London, and not just because Dorset is so much nicer. The line is where the day/night plane intersects the circle, so if we know the green angle, we can work out the number of hours of darkness we have.
Splitting it into two right-angled triangles, we know they each have a hypotenuse of $\cos(51.5º)$ and a base of $\sin(51.5º)\tan(23.5º)$ - so we can work out the angle of each as $\arccos\br{\tan(51.5º)\tan(23.5º)} \approx 58.6º$. The green angle is about 117.2º.
We’re not particularly interested in the angle itself, but rather the fraction of a circle it represents: here, that’s a bit less than a third; dividing by 360º, multiplying by 24 and converting to hours gives 7 hours and 49 minutes – meaning 16 hours and 11 minutes of daylight, which isn’t too far removed from the answer written in stone.
How about Hamburg?
We now have a model: at summer solstice, the number of hours of darkness is:
\(H = \\arccos\\br{\\tan(\\lambda)\\tan(23.5º)} \\times \\frac{24}{180º}\).
I’d generally rewrite that, as I have a mild allergy to arccosines:
\[\\cos(H \\times 7.5º) = \\tan(\\lambda)\\tan(23.5º)\]This also means we can easily work from either side to find $\lambda$ given $H$ or vice-versa.
Now, the writing on the wall says that Hamburg’s longest day is 19 hours - so just five hours of darkness. Does that check out?
$\cos(37.5º) = \tan(\lambda)\tan(23.5º)$
That give $\tan(\lambda) \approx 1.824$, and $\lambda \approx 61.3º$, putting Hamburg just south of the Arctic Circle. That seems… slightly off.
That’s not my Hamburg! Its latitude is too northerly!
According to worldatlas.com, Hamburg’s latitude is more like 53.6º - roughly level with Manchester.
We can work out the maximum day length there, too: if $ \cos(H \times 7.5º) = \tan(53.6º)\tan(23.5º)$, we get 7 hours and 10 minutes of darkness, which is 16 hours and 50 minutes.
According to The US Navy, the true answer is 17 hours - again, off by about 10 minutes ((I believe this is due to how the sunlight refracts through the atmosphere, but that’s physics.)).
I don’t know how long the stone has been up at Durlston Castle, but if I were them, I’d be taking it back for a refund.
* After a request from Quantum Mechanic, I’ve transcribed the writing:
Duration of Longest Day: At London: 16hrs 30mins Hamburg: 19 0 Spitzbergen: 3 1/2 months The Poles: 6 [months]
Clock Times of the World
These differ from Greenwich 4 mins every degree When 12 o’clock noon at Greenwich, it is
East
West
PM
AM
At Paris 12 9
At Swanage 11 52
Rome 1 50
Edinburgh 11 47
Vienna 1 6
Dublin 11 35
Calcutta 5 54
New York 7 4? ((Cut off in the photo, sorry))
* Edited 2018-02-14 to fix some LaTeX.
