Dictionary of Mathematical Eponymy: The Ueda Attractor
What is a Ueda Attractor?
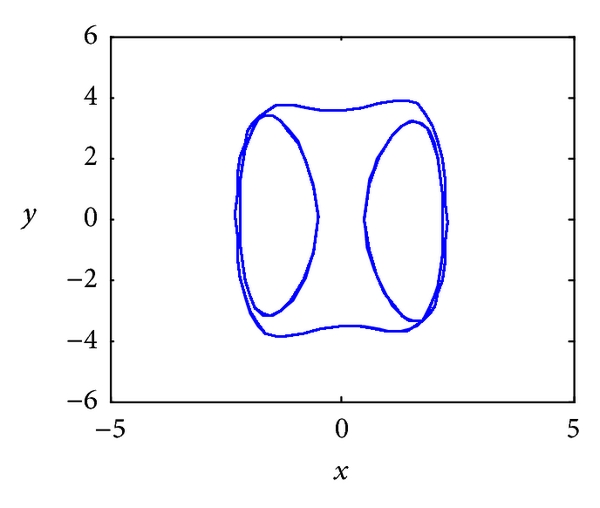
It looks like this. Pretty, huh?
It’s a phase solution of the Duffing equation $\ddot x + 0.05 \dot x + x^3 = 7.5\cos(t)$. It is a strange attractor – it is not periodic, but it is dense (and nearby trajectories converge into it).
Why is it interesting?
I know I said in the last post that fluid dynamics is always interesting, but chaos theory knocks FD into a trumpet of infinite surface area.
I love chaos theory’s origin story (the whole Lorenz/butterfly affair, one of the stories my Uncle Bill told me that set me on a mathematical course). The thing is, I’m not certain Lorenz got there first.
It’s a bit hard to pin down the birthdate of the butterfly – I haven’t got any better than “the winter of 1961” and a suggestion that this means the winter at the end of 1961; Ueda recorded the output of a numerical simulation with chaotic solution in late November 1961. His plot is kept at the Brookhaven National Laboratory in the US, and is regarded as the oldest existing chaotic data.
Who is Yoshisuke Ueda?
Yoshisuke Ueda was born in Kobe, Japan in 1936. He studied at Kyoto University, gaining a Bachelor’s degree in 1959, a Master’s in 1961 and a PhD in 1965. He became a full professor in 1985.
(Reference: Kehui Sun, A Di-li Duo Li-kun, Yanqing Dong, Huihai Wang, and Ke Zhong; Multiple Coexisting Attractors and Hysteresis in the Generalized Ueda Oscillator; Mathematical Problems in Engineering 2013. http://dx.doi.org/10.1155/2013/256092)
* Edited 2022-10-10 to add missing image and reference thereto. Thanks, Andrew!