Getting things wrong, together
This is a guest post by James Grime, all-round maths superstar, with whom it is impossible to have a conversation without someone demanding a selfie or an autograph. He disagrees with my telling of the story of the Truchet debacle and I’m happy to let him set the record straight.
If you want to see maths in new and interesting ways, you should visit MathsCity, the new maths discovery centre in Leeds. Like a science discovery centre, there are lots of physical, hands-on exhibits, but it’s all about maths. There are puzzles to solve, and games to play, and you get to stand inside a giant bubble! You will also find a giant set of Truchet blocks, with which you can make fun blobby patterns.

It’s fun to make blobby patterns. You can try to stack them into cubes and see if you can connect all the blobs. And if you want to get serious about it, you can talk about material like sandstone, which look very much like a Truchet pattern, and the maths behind that recently won the Fields medal.
Or, you can just make blobby patterns.
In fact, I was tasked to design this set of Truchet cubes for MathsCity. So, naturally, my question was, how many Truchet cubes are there? After some work, I was convinced the answer was 16, and so we made a complete set of 16 Truchet cubes.
However, it just so happened that Colin Beveridge ((Hey! That’s my name! - Ed)) was considering the same problem and was equally convinced the answer was 10. One of us had to be wrong. One mathematician would be victorious and the other covered in shame.
It turned out we were both wrong.
My approach had caused me to overcount the number of solutions, while Colin’s approach had caused him to undercount the number of solutions. It was only by comparing our two approaches did we see our own mistakes, and finally settle on the correct number.
My approach was ridiculously overcomplicated. I started with the fact that each face was a Truchet tile. That means, each face was either a square with quarter-circles in the top left corner and the bottom right corner, or the same tile but rotated 90degrees. I called these two tiles 0 and 1.


I then imagined a cube, flattened into a net, and filled the six faces with either the 0-tile or the 1-tile. You could think of these six faces as a six-digit binary number from 0 to 63. But some of these cubes were equivalent. In other words, rotating the cube might give us one of the other solutions. So I went through each possibility, and thought about how the 24 possible rotations would affect the cube’s binary number. This resulted in eight non-equivalent cubes.

Finally, all I had to do was to colour in the cubes. For example, I could colour the cubes black and white. Or I colour the same cube with those two colours swapped over. That would give me two possible colourings for each cube to make a total of 16 cubes.
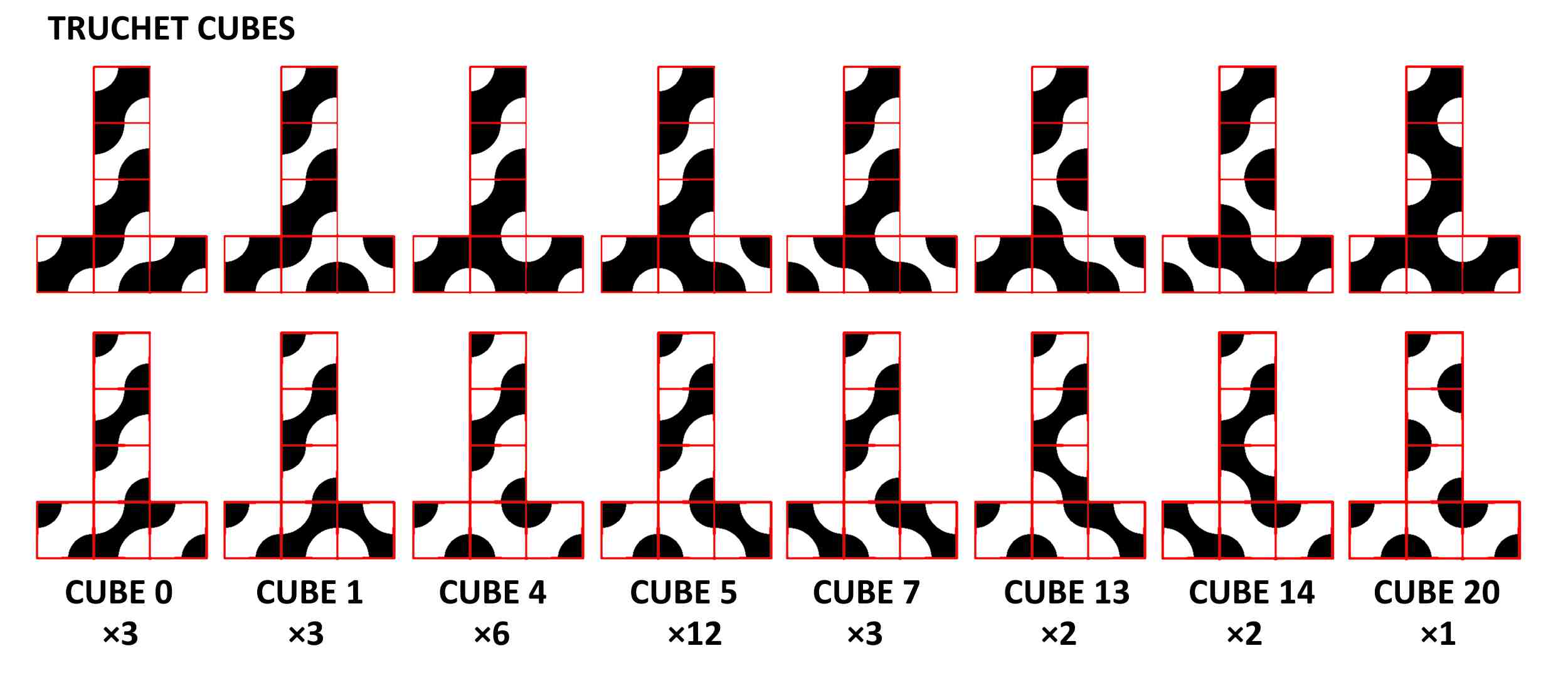
Colin’s approach to the same problem was much simpler. Colin started with the tiles already coloured in. In that case, each face can be thought of as a tile with a black stripe, or a tile with a white stripe.


Now the question just becomes, what does a cube look like with 0 black stripes, 1 black stripe, 2 black stripes, and so on. After a bit of thought, Colin found ten possibilities.
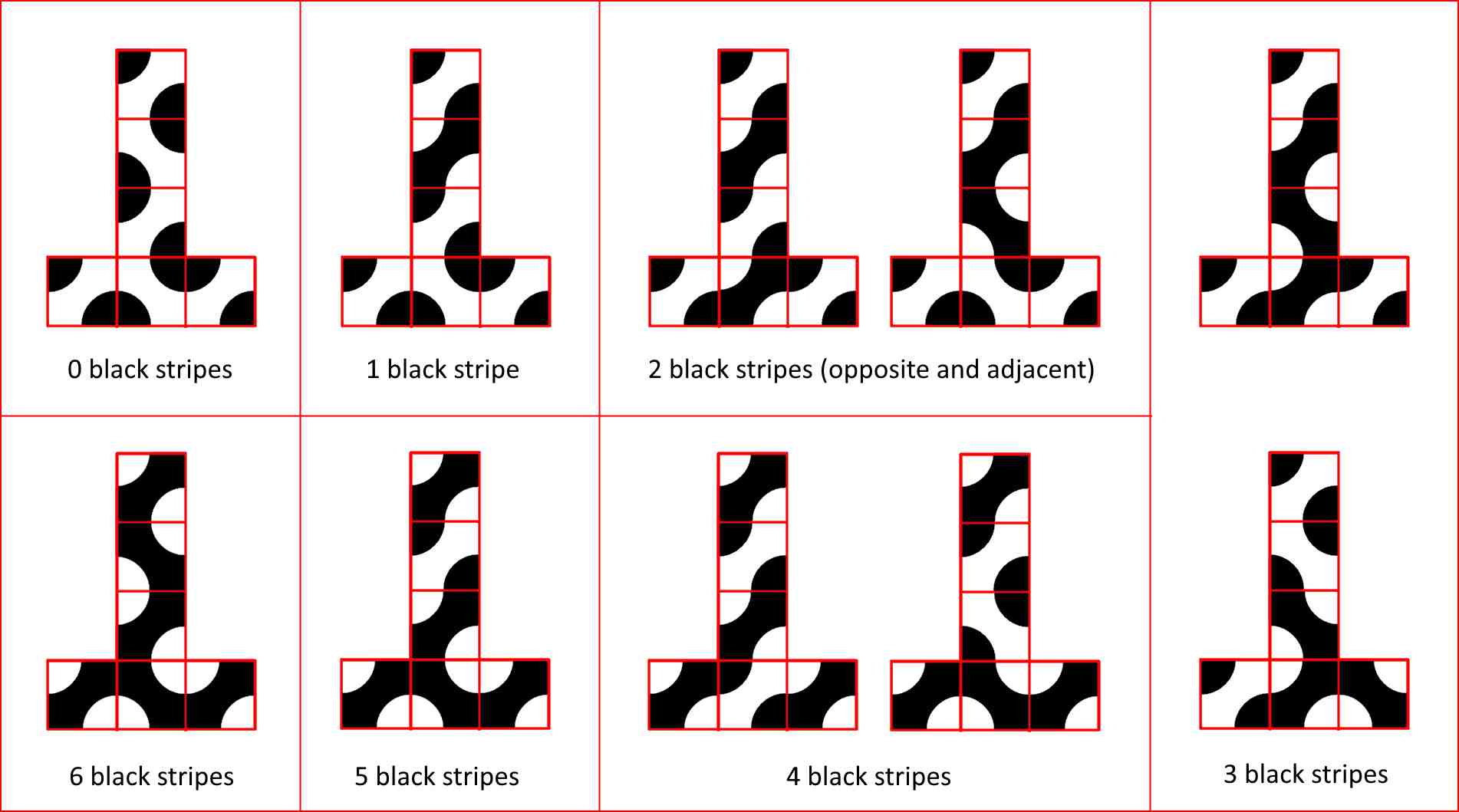
When I saw Colin’s solution, I was worried. It was far more elegant than mine, and that it had a completely different answer. I went back and checked my solution. And yes, it appeared that I had overcounted. In fact, all cubes with three black stripes are self-inverse – if we swap the two colours we get the same cube.
But if that’s true, then the total number of non-equivalent Truchet cubes should be 12, and not the 10 Colin had. It turns out Colin had also missed a subtlety with the cube with three stripes as well. The three black stripes can either line-up to make one long stripe, or they can meet at a corner. But there are two versions of the cubes with long stripes, and two ways three stripes can meet at corner (one where they meet at the corner, and one where they make a “hole” at the corner).
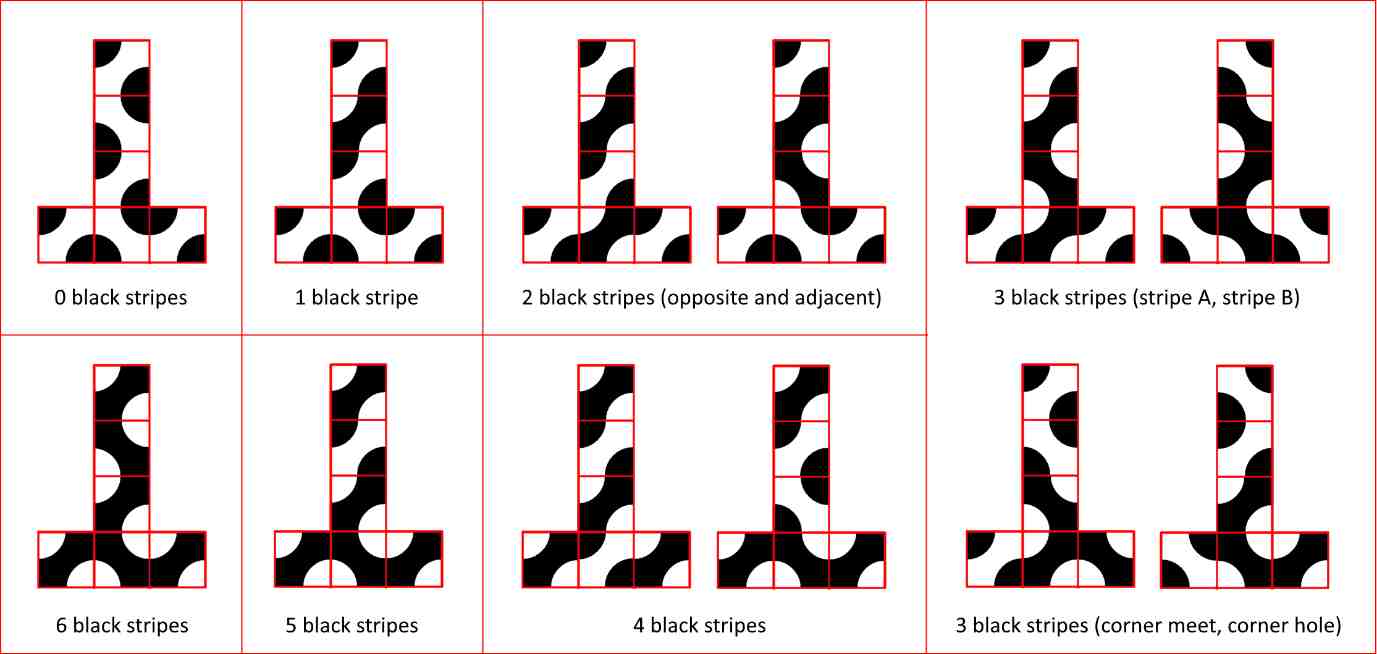
This turned out to be a really nice puzzle to solve. It’s not too hard, with scope to solve it in different ways, but with some subtleties that stop it being completely straightforward. It certainly fooled me and Colin, and we might be mega-geniuses, so it must have been hard.
Well, not really. There were faults in both our efforts. But by comparing our solutions and combining our approaches, we might make one mega-genius.
- James Grime is a mathematician, lecturer and public speaker based in Cambridgeshire. You can read more about his workshops and talks and book him to speak here