Rote vs readiness
In a class recently, I came across a circle theorem problem I’m certain I’ve seen before, but that I didn’t know off the top of my head how to solve. Here it is; have a go at it if you’d like to.
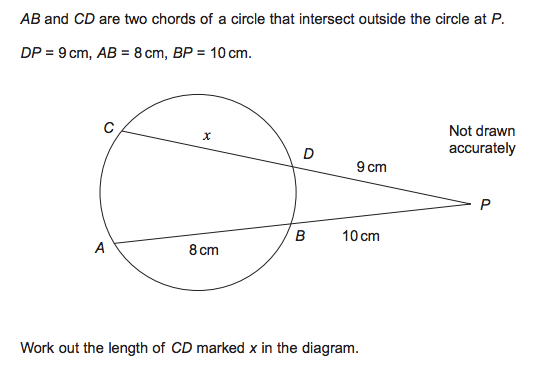  The examiners’ expectation was clearly that the student would know that PD:PA = PB:PC - and neither she nor I did. If you’ve learned the circle theorems by rote, congratulations: if you didn’t have this one on your list, you’re stuck. However, if you’ve played around with them, you’re in luck.
 The examiners’ expectation was clearly that the student would know that PD:PA = PB:PC - and neither she nor I did. If you’ve learned the circle theorems by rote, congratulations: if you didn’t have this one on your list, you’re stuck. However, if you’ve played around with them, you’re in luck.
You might say: I can draw a butterfly by adding the line segments CB and DA. Then I know angles DAP and BCP are the same size - which means PBC and PDA are similar triangles. (Do you see why?)
The side PD in PDA corresponds to the side PB in PBC, so PBC is $\frac{10}{9}$ as big as PDA. Since PA is a convenient 18cm long, that means PC is 20cm and $x$ has to be 11cm.
When a short list you know how to use beats a long list that’s incomplete
I know a few circle theorems. They’re my canonical example of things to know for the exam that will be no use to you ever, although I once advised a friend to use one to find the centre of a circle he’d drawn, and I’m told they can be used by rugby place-kickers to find the best angle to kick at goal.
I don’t know every circle theorem, by a long shot. (Every so often, someone shows me something circle-related and I go “wow!” before forgetting it instantly.) But what I can do is work problems out from first principles when I don’t know.
And that, in a nutshell, is what I think is the major difference between the “chant your times tables” school of thought and my idea of maths: memorising large lists of facts can get you a long way; a short list you can manipulate to work things out gets you much further.