Tessellations and cuboids
On a recent ((recent, at least, as I’m writing this; by the time it gets to your screen, it’ll be months ago)) episode of Wrong, But Useful, Dave mentioned something interesting ((pause for readers to insert own joke)): if you take three regular shapes that meet neatly at a point - for example, three hexagons, or a square and two octagons - and make a cuboid whose edges are in the same ratio as the number of sides on each shape (e.g., 6 by 6 by 6 or 4 by 8 by 8), the resulting cuboid has a volume that’s (numerically) the same as its surface area (here, 216 or 256).
Let’s prove it!
The interior angle of a regular $n$-gon is $\pi - \frac{2n}{\pi}$, or $180 - \frac{360}{n}$ if you insist on silly angle measures. In fact, it’s probably better to think of it as $\frac{n-2}{2n}$ of a circle, in any case.
To have three regular shapes - let’s call them an $i$-gon, a $j$-gon and a $k$-gon - meeting at a point, the angles would need to make a whole circle: $\frac{i-2}{2i} + \frac{j-2}{2j} + \frac{k-2}{2k} = 1$
Those fractions don’t look very nice, do they? Let’s carefully multiply everything by $2ijk$ to get rid of them:
$(ijk - 2jk) + (ijk - 2ik) + (ijk - 2ij) = 2ijk$
Rearranging: $ijk = 2(ij + jk + ki)$.
The left-hand side is the volume of the resulting cuboid, and the right-hand side is its surface area. $\blacksquare$.
I like that a lot
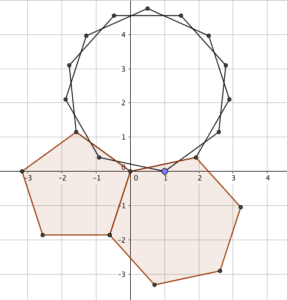
It’s a surprising result with a proof that drops out really neatly. One neat thing: it also works (with a bit of definition-stretching) for fractional shapes. If, for example, you made a tesselation comprising a regular pentagon, a regular hexagon and a regular 7.5-gon, this too would satisfy the constraints: $(5)(6)(7.5) = 225 = 2((5)(6)+(5)(7.5)+(6)(7.5))$.
I’m not sure what a regular $\pi$-gon would look like (other than a mess), but one could construct something a similar example with irrational numbers.