The Angle Windmill
One of the places I would always fall down in A-level mechanics was on inclined plane force diagrams: I was chronically incapable of putting the correct angle in the correct place.
Until, that is, I figured out…
The Angle Windmill
It looks like this: 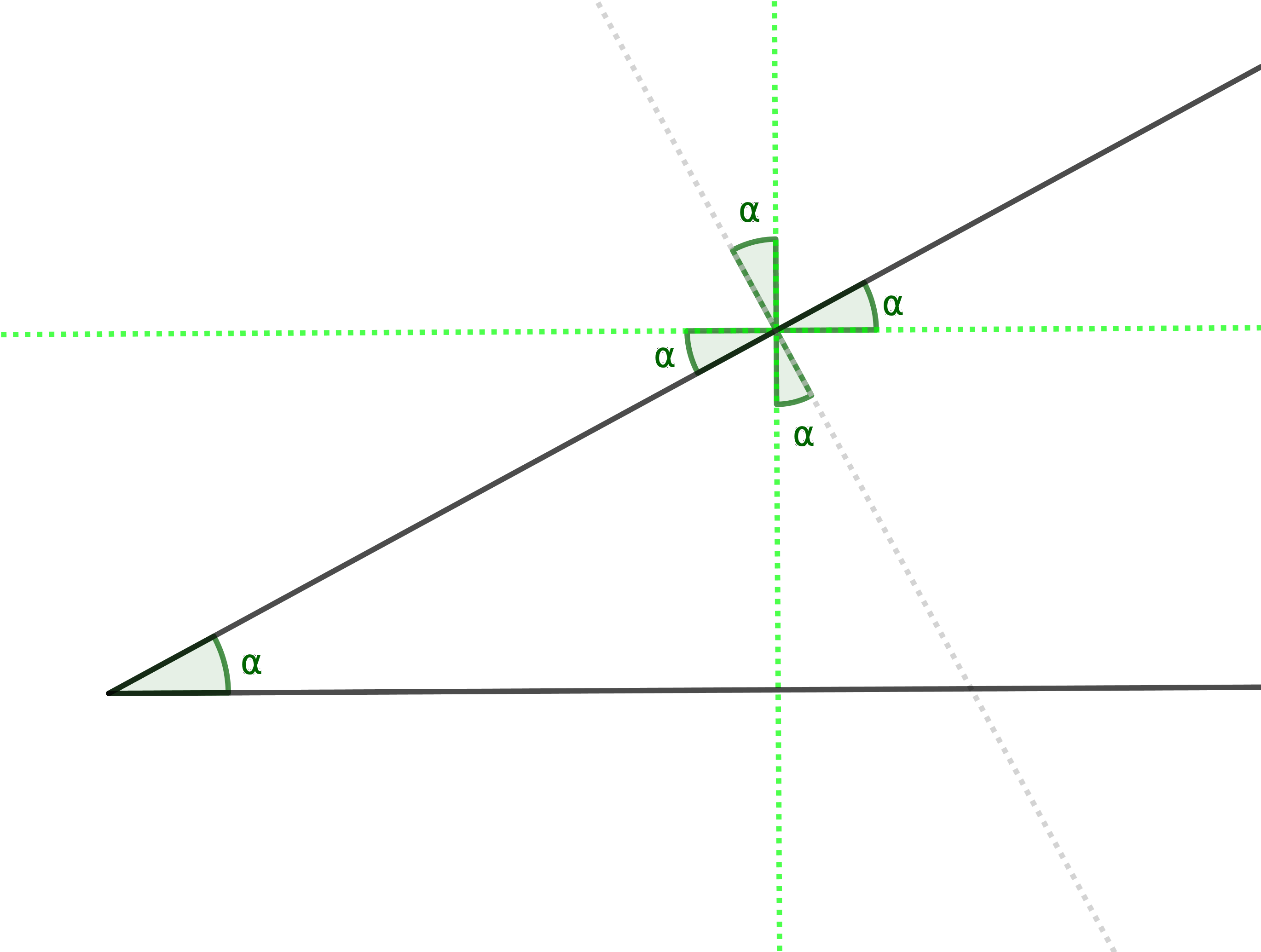
The process goes as follows:
- Draw a big diagram without any forces on
- Mark the angle between the plane and the horizontal as $\alpha$
- Draw a line perpendicular to the inclined plane (in grey on the diagram) through your object
- Draw a horizontal and vertical line (in green) through the object
- (You now have eight rays coming out of the object
- Find and mark a pair of rays separated by $\alpha$
- Mark alternate spaces between rays with $\alpha$
Boom! Job done. Now you know which angle goes where. You might alsonote that the angles in the gaps are all $90º - \alpha$.
But wait. There’s more.
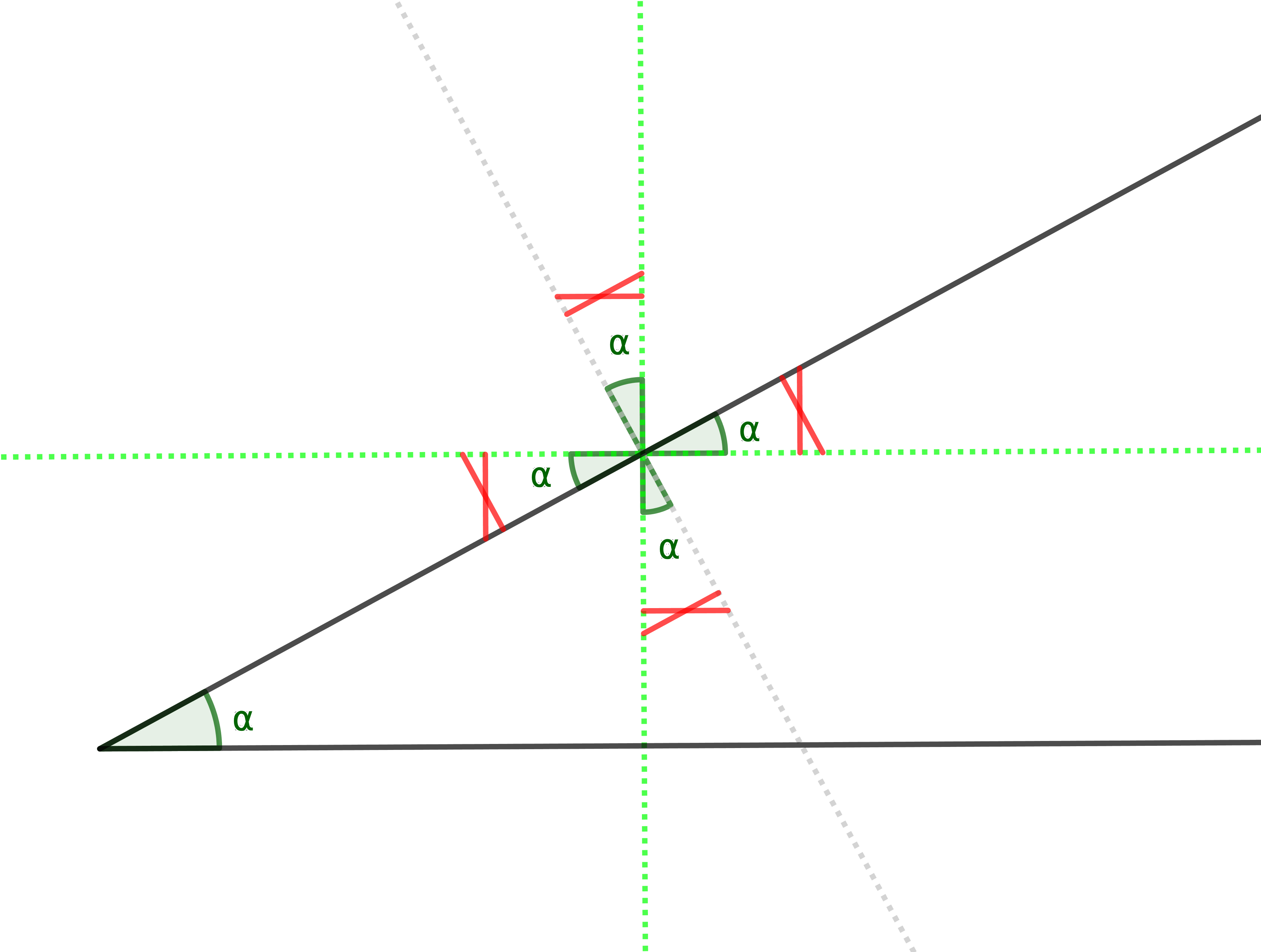
Suppose you need to resolve a force that lies on one perpendicular grid to the other.
If you draw the sails on the windmill like this, it tells you which component of the force you’re resolving requires a sine.
This is, of course, a lazy shortcut – working out the trig isn’t that hard. It’s just easy to get wrong in a hurry, and I was always in a hurry.
(You may like, as an exercise, to convince yourself that all of the assertions in this post are true.)