”$\sin(15º)$,” said the GCSE student, and the Mathematical Ninja – recognising that the qualification recognised idiotic angle measures – let it slide.

“0.2588”, they muttered, under their breath, knowing full well that the exact answer – $\frac{\sqrt{6} - \sqrt{2}}{4}$ – would get them a blank stare. They sighed the sigh of a defeated ninja, and noted that $\cos(75º)$ was 0.9659.

“How do you know that?” asked the student, brightly.

The Mathematical Ninja froze – their spidey senses tingled. Was it a trap? Was the student simply trying to derail the class by getting them to talk about mental arithmetic rather than the lesson at hand? They decided it was a risk they was prepared to take. “Have you heard of Ailles’ Rectangle?” they asked.

The student shook his head.

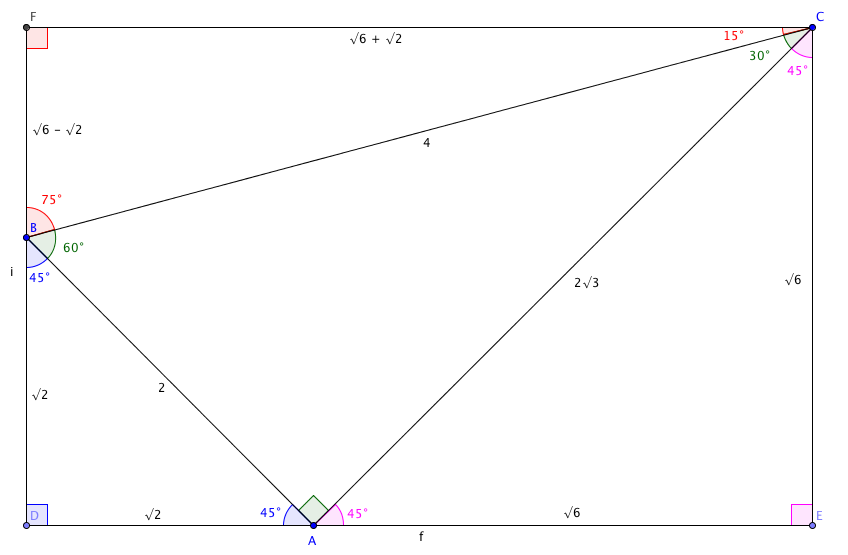
“It looks like this:”

Ailles' Rectangle

“In honesty, sensei, that doesn’t clear much up for me.”

“Fine, allow me to explain. The triangle in the middle – with the green angles – is half of an equilateral triangle.”

“Oh yes – it’s 30-60-90, like the set square.”

“Right. I’ve chosen a hypotenuse of 4, which will keep the numbers relatively clean.”

“I know the shorter… leg, do you call it? is 2 units, and Pythagoras says the other side is $2\sqrt{3}$.”

“You read that off the picture, didn’t you?”

“Well, obviously.”

“Anyhow. It’s set up so you have two (ahem) 90-45-45 triangles at the bottom edge, either side of the right angle.”

“I can see that, the blue one and the pink one – and I can use Pythagoras again to get the shorter sides – $\sqrt{2}$ in the blue triangle and $\sqrt{6}$ in the big one. That means I know the length of the sides of the rectangle – it’s $\sqrt{6} + \sqrt{2}$ long, and $\sqrt{6}$ tall.”

“Good. And as for the top triangle?”

“The top right angle has to be 15º, because that’s what’s left over from the right angle. The bottom left angle has to be 75º. The top side is $\sqrt{6} + \sqrt{2}$, because it’s the top side of the rectangle, and the left side is $\sqrt{6} - \sqrt{2}$, because it’s the rectangle’s height minus the blue triangle.”

“Go on?”

“So $\sin(15º) = \frac{\sqrt{6} - \sqrt{2}}{4}$, which presumably is 0.2588, I think you said.”

“I did,” said the Mathematical Ninja.

“But how did you know that?”

“Allow me,” said the Mathematical Ninja, “some mysteries,” as they surreptitiously turned the Wolfram|Alpha app off on their phone.

  • Edited 2021-01-02 to give the Mathematical Ninja the correct gender.